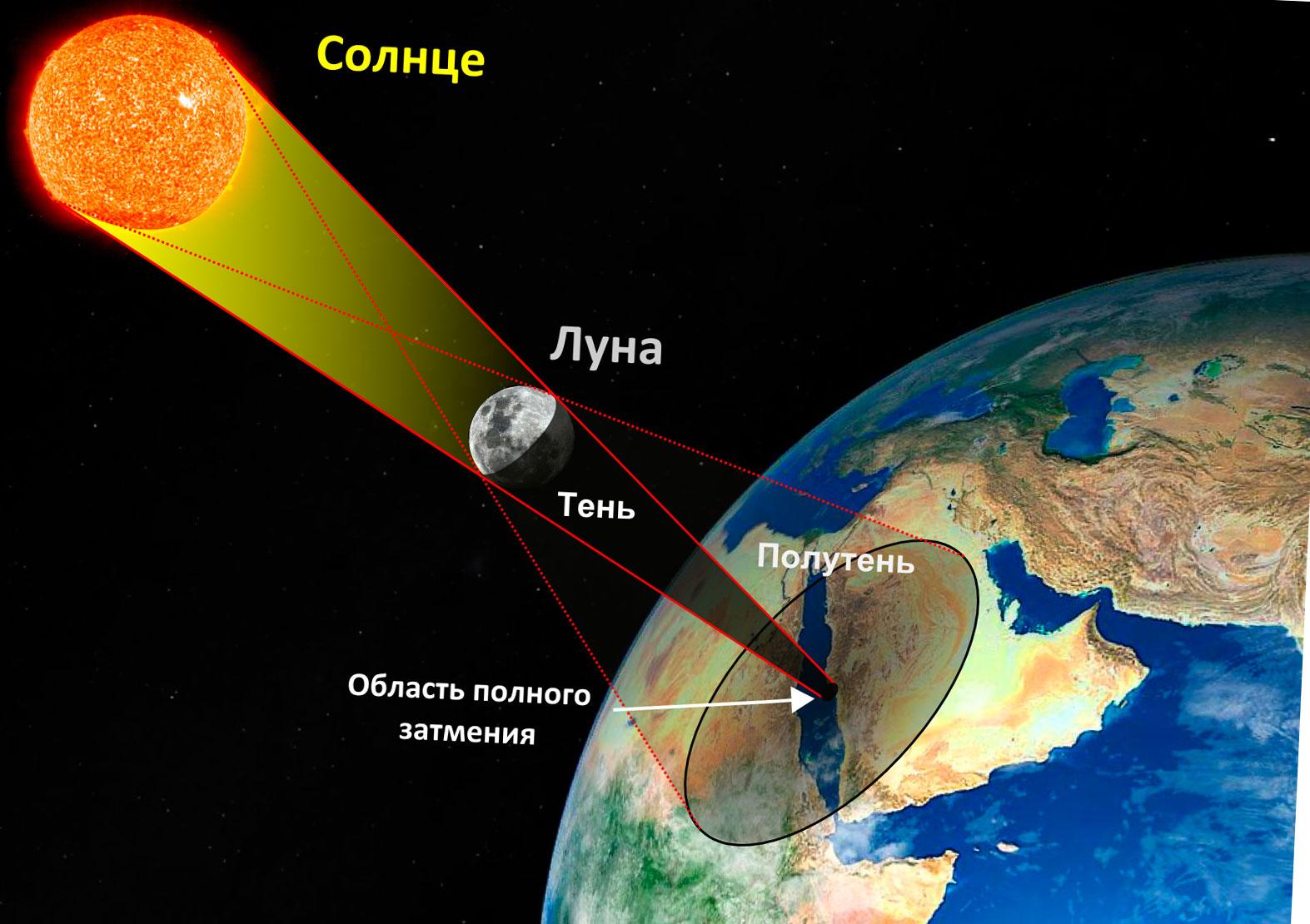
Обоени квадрати и затемнувања на Сонцето

Статијата ги опишува моите часови за средношколци - стипендисти на Националниот детски фонд. Фондацијата бара особено надарени деца и младинци (од XNUMX одделение основно училиште до средно училиште) и нуди „стипендии“ на избрани ученици. Сепак, тие воопшто не се состојат во подигање готовина, туку во сеопфатна грижа за развој на талентот, по правило, во текот на многу години. За разлика од многу други проекти од овој тип, познати научници, културни дејци, истакнати хуманисти и други мудри луѓе, како и некои политичари, сериозно ги сфаќаат одделенијата на Фондацијата.

Активностите на Фондацијата се прошируваат на сите дисциплини кои се основни училишни предмети, освен спортот, вклучително и уметноста. Фондот е создаден во 1983 година како противотров на тогашната реалност. Во фондот може да се пријави секој (најчесто преку училиште, по можност пред крајот на учебната година), но, секако, има одредено сито, одредена процедура за квалификација.

Како што веќе спомнав, написот се базира на моите мастер-класови, поточно во Гдиња, во март 2016 година, во 24-та помлада гимназија при III гимназија. Морнарица. Долги години овие семинари се организирани под покровителство на Фондацијата од Војчех Томалчик, учител со извонредна харизма и високо интелектуално ниво. Во 2008 година влезе во првите десет во Полска, на кои им беше доделена титулата професор по педагогија (предвидена со закон пред многу години). Има мало претерување во изјавата: „Образованието е оската на светот“.

и месечината се секогаш фасцинантни - тогаш можете да почувствувате дека живееме на мала планета во огромен простор, каде што сè е во движење, мерено во сантиметри и секунди. Дури и малку ме плаши, а и временската перспектива. Дознаваме дека следното целосно затемнување, видливо од областа на денешна Варшава, ќе биде во ... 2681 година. Се прашувам кој ќе го види? Очигледните големини на Сонцето и Месечината на нашето небо се речиси исти - затоа затемнувањата се толку кратки и толку спектакуларни. Со векови, тие кратки минути треба да бидат доволни за астрономите да ја видат сончевата корона. Чудно е што се случуваат двапати годишно... но тоа само значи дека некаде на Земјата можат да се видат на краток временски период. Како резултат на приливите движења, Месечината се оддалечува од Земјата - за 260 милиони години ќе биде толку далеку што ние (ние???) ќе гледаме само прстенести затемнувања.

Очигледно првиот што предвиде затемнувањето, бил Талес од Милет (28-585 век п.н.е.). Веројатно нема да знаеме дали тоа навистина се случило, односно дали тој го предвидел, бидејќи податокот дека затемнувањето во Мала Азија се случило на мај 567 година 566 година п.н.е е факт потврден со современите пресметки. Се разбира, наведувам податоци за денешното пресметување на времето. Кога бев дете, замислував како луѓето бројат години. Така, ова е, на пример, XNUMX п.н.е., доаѓа новогодишната ноќ и луѓето се радуваат: само XNUMX години п.н.е.! Колку само мора да биле среќни кога конечно дојде „нашата ера“! Каков пресврт од милениуми доживеавме пред неколку години!

Математика за пресметување датуми и опсези затемнувањата, не е особено комплицирано, но е преполно со секакви фактори поврзани со регуларноста и, уште полошо, со нерамномерното движење на телото во орбитите. Дури би сакал да ја знам оваа математика. Како можел Талес од Милет да ги направи потребните пресметки? Одговорот е едноставен. Мора да имате мапа на небото. Како да се направи таква мапа? Ова исто така не е тешко, старите Египќани знаеле како да го направат тоа. На полноќ, двајца свештеници излегуваат на покривот на храмот. Секој од нив седнува и црта што гледа (како колегата). По две илјади години, знаеме сè за движењето на планетите ...

Прекрасна геометрија или забава на „чергата“

Грците не ги сакаа бројките, тие прибегнаа кон геометријата. Ова е она што ќе го направиме. Нашиот затемнувањето тие ќе бидат едноставни, шарени, но исто толку интересни и реални. Ја прифаќаме конвенцијата дека сината фигура се движи на таков начин што ја затемнува црвената. Сината фигура да ја наречеме месечина, а црвената фигура сонце. Си ги поставуваме следниве прашања:

1. колку долго трае затемнувањето;
2. кога половина од целта е покриена;

   Ориз. 1 Повеќебоен „тепих“ со сонцето и месечината

3. која е максималната покриеност;
4. дали е можно да се анализира зависноста на покриеноста на штитот на време? Во оваа статија (ограничен сум со количината на текст) ќе се фокусирам на второто прашање. Зад ова е убава геометрија, можеби без здодевни пресметки. Ајде да погледнеме на сл. 1. Дали може да се претпостави дека ќе биде поврзан со ... затемнување на Сонцето?

Морам искрено да кажам дека задачите за кои ќе разговарам ќе бидат специјално избрани, прилагодени на знаењата и вештините на средношколците и средношколците. Но, ние тренираме на такви задачи како што музичарите свират вага, а спортистите прават општи вежби за развој. Освен тоа, нели е само убав килим (сл. 1)?

Ориз. 2 „Сина“ Месечина и „Црвено“ Сонце

Нашите небесни тела, барем на почетокот, ќе бидат обоени квадрати. Месечината е сина, сонцето е црвено (најдобро за боење). со сегашноста затемнувањето Месечината го брка сонцето по небото, го стигнува ... и го затвора. Така ќе биде и кај нас. Наједноставниот случај, кога Месечината се движи во однос на Сонцето, како што е прикажано на сл. 2. Затемнувањето започнува кога работ на дискот на Месечината ќе го допре работ на Сончевиот диск (сл. 2) и завршува кога ќе оди подалеку од него.

Ориз. 3 Месечината дијагонално се приближува кон сонцето

Претпоставуваме дека „Месечината“ поместува една ќелија по единица време, на пример, во минута. Затемнувањето потоа трае осум единици време, да речеме минути. Половина затемнувања на Сонцето целосно затемнет Половина од бирачот се затвора двапати: по 2 и 6 минути. Графикот на процентуално заматување е едноставен. Во текот на првите две минути, штитот се затвора рамномерно со брзина од нула до 1, а следните две минути е изложен со иста брзина.

Еве еден поинтересен пример (сл. 3). Месечината дијагонално се приближува кон сонцето. Според нашиот договор за плаќање во минута, затемнувањето трае 8√2 минути - во средината на ова време имаме целосно затемнување. Да пресметаме кој дел од сонцето е покриен по времето t (сл. 3). Ако поминале t минути од почетокот на затемнувањето, и како резултат на тоа Месечината е како што е прикажано на сл. 5, тогаш (внимание!) Затоа, таа е покриена (површината на квадратот APQR), еднаква на половина од сончевиот диск; затоа, беше покриена кога, т.е. по 4 минути (потоа 4 минути пред крајот на затемнувањето).

Ориз. 4 График на функцијата „засенчување“.

Тоталитет трае еден момент (t = 4√2), а графикот на функцијата „засенчен дел“ се состои од два лака на параболи (сл. 4).

Нашата сина месечина ќе го допре аголот со црвеното сонце, но ќе го покрие, одејќи не дијагонално, туку малку дијагонално.Интересна геометрија се појавува кога малку ќе го комплицираме движењето (сл. 6). Насоката на движење сега е векторски [4,3], односно „четири ќелии надесно, три ќелии нагоре“. Положбата на Сонцето е таква што затемнувањето започнува (позиција А) кога страните на „небесните тела“ се спојуваат на четвртина од нивната должина. Кога Месечината ќе се пресели во положбата Б, ќе затемни една шестина од Сонцето, а во положбата C ќе затемни половина. Во позиција D, имаме целосно затемнување, а потоа сè се враќа назад, „како што беше“.

Ориз. 5 Дел од Сонцето скриен во времето т

Затемнувањето завршува кога Месечината е во положбата G. Тоа траело онолку колку што должина на делот AG. Ако како и досега го земеме како единица време времето во кое Месечината минува „еден квадрат“, тогаш должината на АГ е еднаква. Ако се вратиме на старата конвенција дека нашите небесни тела се 4 на 4, резултатот би бил поинаков (што?). Како што е лесно да се прикаже, целта се затвора по t < 15. Графикот на функцијата „процент на покриеност на екранот“ може да се види на сл. 6.

Ориз. 6 График на функцијата „процентна заштита“.

Равенка за затемнување и скок

Ориз. 7 Попречување на сончевиот диск за време на затемнувањето прикажано на сл. 6

Проблемот со затемнувањата би бил нецелосен доколку не го разгледаме случајот со круговите. Ова е многу покомплицирано, но ајде да се обидеме да откриеме кога еден круг затемнува половина од другиот - и во наједноставен случај, кога еден од нив се движи по дијаметарот што ги поврзува и двете. Цртежот им е познат на имателите на некоја кредитна картичка.

Пресметувањето на положбата на полињата е комплицирано, бидејќи бара, прво, познавање на формулата за плоштина на кружен сегмент, второ, познавање на лакот на аголот и трето (и најлошо од сè), способност да реши одредена равенка за скокање. Нема да објаснам што е „преодна равенка“, ајде да погледнеме на пример (сл. 8).

Ориз. 8 „Сферично“ затемнување

Кружен пресек е „садот“ што останува по сечењето круг со права линија. Областа на таков сегмент е S = 1/2r²(φ-sinφ), каде што r е радиусот на кругот, а φ е централниот агол на кој лежи отсечката (сл. 8). Ова лесно се добива со одземање на површината на триаголникот од областа на кружниот сектор.

Епизода О₁O₂ (растојанието помеѓу центрите на круговите) тогаш е еднакво на 2rcosφ/2, а висината (ширина, „струкот“) h = 2rsinφ/2. Значи, ако сакаме да пресметаме кога Месечината ќе покрие половина од сончевиот диск, треба да ја решиме равенката: која, по поедноставувањето, станува:

Ориз. 9 Графикони на две функции

Решението на таквите равенки е надвор од опсегот на простата алгебра - равенката ги содржи и аглите и нивните тригонометриски функции. Равенката е надвор од дофатот на традиционалните методи. Затоа се вика да скокне. Ајде прво да ги погледнеме графиконите на двете функции, односно функциите и функциите.Од оваа слика можеме да прочитаме приближно решение. Како и да е, можеме да добиеме итеративна апроксимација или... да ја користиме опцијата Решавач во табелата на Excel. Секој средношколец треба да може да го прави ова, бидејќи е 20 век. Користев пософистицирана алатка Mathematica и еве го нашето решение со XNUMX децимални места со непотребна прецизност:

SetPrecision[FindRoot[x==Sin[x]+Pi/2,{x,2}],20] {x⇒2.3098814600100574523}.

Ориз. 10 Анимација на затемнување во математика

Ова го претвораме во степени со множење со 180/π. Добиваме 132 степени, 20 минути, 45 и четвртина лак секунда. Пресметуваме дека растојанието до центарот на кругот е О₁O₂ = 0,808 радиус, и „струк“ 2,310.